The order of nucleotides in a sequence is governed not only by the encoded information, but also by physical and biological constraints (see reference). All sections of the genome should be exposed to the same constraints and consequently should have similar fingerprints of oligonucleotide frequencies, i.e. frequencies being consistently either low or high for the same oligonucleotide. The frequency of each oligonucleotide from 2 to 7-mers is indeed approximately the same throughout the genome. However, there are always some regions which exhibit an atypical oligonucleotide composition, indicating that this DNA has been exposed to particular constraints other than those seen in the bulk of the genome.
To characterize OU in a sequence, the concept of OU patterns has been introduced that is a table of relative frequencies of words of length N calculated by applying different schemes of normalization by the constituent shorter words. Different types of OU patterns were abbreviated as type_Nmer. Types were “n0” for non-normalized, “n1” for normalized by mononucleotide frequencies, “n2” for normalized by dinucleotides and so on. Each OU pattern is characterized by three statistical parameters: D – distance between two patterns of the same type; PS – pattern skew, distance between the two patterns of the direct and reverse strands of the same DNA sequence; and RV – oligonucleotide usage variance.
The nomenclature is hence as follows: distance between a local n0_4mer pattern and the corresponding global pattern – n0_4mer:D; pattern skew of a n0_4mer pattern – n0_4mer:PS; variance of a n1_4mer pattern normalized by frequencies of mononucleotides in an analyzed genome fragment – n1_4mer:RV; variance of a n1_4mer pattern normalized by frequencies of mononucleotides in a complete genome – n1_4mer:GRV.
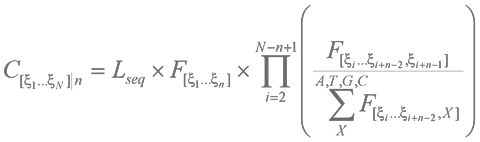
D[x1…xN]
= (C[x1…xN]|obs -
C[x1…xN]|e )
/ C[x1…xN]|0
where xn is any nucleotide A, T, G or C at the position 1, 2, 3, … N in the N-long word; C[x1…xN]|obs is the observed count of the word, [x1…xN]; C[x1…xN]|e is the expected count and C[x1…xN]|0 is a standard count estimated from the assumption of an equal distribution of words in the sequence: (C[x1…xN]|0 = Lseq ´ 4-N).
OU parameters of words of length N may be normalized by shorter words n ( 0 £ n < N). C[x1…xN]|e = C[x1…xN]|0 if OU is not normalized, or C[x1…xN]|e = C[x1…xN]|n if OU is normalized by empirical frequencies of all shorter words of the length n. The normalization was performed as follows. First of all, we calculated observed frequencies F[x1…xn] of n-long words in the sequence. Each word of length N can be represented as a consecutive set of N – n + 1 overlapping component words of length n. For example, a pentamer ATGGC can be expressed as a set of 4 overlapping dimers: AT, TG, GG and GC. In a general case of a N-long word, a component word [x1…xn] reduces the set of available options for the next word in the sequence to 4 possible oligonucleotides: [x2…xn,A], [x2…xn,T], [x2…xn,G] and [x2…xn,C]. The relative frequencies of these words are:
F[x2…xn,xn+1] ´ [ (F[x2…xn,A] +F[x2…xn,T] +F[x2…xn,G] +F[x2…xn,C]) ]-1
whereby the F values are the observed frequencies of the particular word of length n in the complete sequence and x is any nucleotide A, T, G or C. The expected count of a word [x1…xN] of length N in a Lseq long sequence normalized by frequencies of n-mers (n < N) was calculated as follows:

Two subtypes of normalization of local OU patterns were defined: normalized by frequencies of component words in the current genomic fragment (internal normalization, by default) and in the complete sequence of the genome (generalized normalization, G).
For
further processing of OU
statistics, the words were sorted by their D[x1…xN]
and the ranks of words instead the real values of deviations of
observed from
expected counts were used. The rank values (from 1 to
Distances
between patterns <D>
The distance D between two patterns was calculated as the sum of absolute distances between ranks of identical words (w, in a total 4N different words) in patterns i and j as follows:
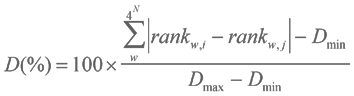
The program calculates distances for 4 possible combinations of the plus/minus DNA strands and selects the minimal value as the distance. Distances are normalized by the value of the maximally possibles distance between patterns of this type. Dmax = 4N(4N – 1)/2 and Dmin = 0 in this case. Normalization makes it possible to compare patterns of different word length (4mer to 3mer or 5mer patterns, for example). The distance between two OU patterns calculated for different genomes reflects phylogenetic relation between these organisms. D values between OU patterns calculated for a horizontally transferred element and for complete genome usually are much higher than D values between patterns calculated for a core genome fragment and the complete genome.
PS is a particular case of D where patterns i and j were calculated for the same DNA but for direct (plus) and reverse (minus) strands, respectively. Dmax = 4N(4N – 1)/2 and Dmin = 4N if N is an odd number or Dmin = 4N – 2N if N is an even number.
A trend to keep PS as low as possible was observed for all bacterial chromosomes (see reference). Contrarily, extremely high asymmetry between OU patterns calculated for two strands of the same DNA fragment was peculiar to viral genomes, phages and some plasmids. This parameter may be used to identify inserted prophage elements in bacterial genomes. Some other genomic loci characterized by extremely high PS correspond to the clusters of genes for ribosomal RNAs.
Oligonucleotide
usage variances <RV> and <GRV>
Variance as a characteristic of an OU pattern was calculated as follows:
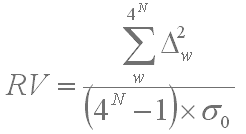
where Dw is a deviation of the real count of the word w in the sequence form the expected count; N is the total number of words of the pattern (4 powered to the length of the word; 44 = 256 words for a tetranucleotide usage pattern); σ0 is the expected standard deviation of the word distribution in a randomly generated sequence that depends on the sequence length and the word length:
σ0=
0.14 + 4N/Lseq
where Lseq is length of the sequence.
As long as Dw depends strongly on the normalization scheme been applied, the RV value is pattern specific. Let us consider the variance calculated for a local n1_4mer pattern normalized by frequencies of mononucleotides in an analyzed genomic fragment (n1_4mer:RV), and the variance of a n1_4mer pattern of the same fragment normalized by frequencies of mononucleotides in a complete genome – global normalization (n1_4mer:GRV). These values may not be the same, and this fact is used for identification of putatively horizontally transferred genomic islands.
Due to the constraints on nucleotide combinations in a real genomic DNA sequence, the RV values of fragments of bacterial DNA are significantly higher than the values calculated for a randomly generated sequence. However, uncontrolled mutations tend to make a constrained sequence similar to a random one, which subsequently equalize the number of oligonucleotides present and thus decreases RV. This is why in a bacterial genome RV values are smaller for the DNA fragments containing unconserved non-coding sequences, remnants of former genes and silenced gene islands. Uncontrolled mutations tend to accumulate in these sequence regions, following their inactivation through, for example, an insertion sequence at a critical position and subsequent relaxation of constraints on DNA sequence.
GC-content and skew <GC>,<AT>,<GCS>,<ATS>
Intragenomic GC-content, AT-content, GC-skew and AT-skew variations were determined as quantities of (G+C), (A+T), (G-C)/(G+C), (A-T)/(A+T) respectively, averaged over a sliding window of certain length.
Users are able analyze their own novel sequences on a local PC. The command line Python program OligoWords is first used to analyse a FASTA or GenBank formatted sequence. The program is available for download in several packages containing precompiled executable files. Since the SWGB is implemented as a Java applet, it can be run within a web browser locally. The HTML-embedded applet SeqWord_Viewer.###.zip is available for download from the same site. The text file output from OligoWords is read into the SWGB via the 'Open' function of the 'File' menu, and the complete functionality of the online system is then available. You can read more about the standalone programs here.